Approach

Deep hashing based (image) similarity search in ElasticSearch
Uses multi index hashing
Seamless integration into ES by terms queries and neighbors index
Advantages:
- Low search latencies: short hash codes for filtering (64 bit)
- High retrieval quality: long hash codes for re-ranking (256 bit)

See https://arxiv.org/abs/2305.04710 and https://github.com/umr-ds/ElasticHash for more details.

Multi-Index Hashing (MIH)

The approach is based on Multi-index hashing. The idea of MIH is based on the following observation: for two binary codes \(h=(h^1,...,h^m)\) and \(g=(g^1,...,g^m)\) where \(m\) is the number of partitions, \(h^k\) and \(g^k\) are the \(k^{th}\) subcodes and \(H\) is the Hamming norm, the following proposition holds:

\[\left \| h - g \right \|_H \leq r \Rightarrow \exists k \in \left \{ 1,...,m \right \} \: \left \| h^k - g^k \right \|_H \leq \left \lfloor \frac{r}{m} \right \rfloor\]

For the case of 64-bit codes that are decomposed into \(m=4\) subcodes, this means that a code is in a Hamming radius \(r < 12\) if at least one of the subcodes has a distance of \(d \leq \lfloor \frac{r}{m} \rfloor = 2\) from the query subcode. The performance of MIH can be increased if the subcodes are maximally independent of each other, especially for shorter codes. Thus, after training a deep hashing model, the bit positions should be permutated accordingly (see decorrelate()).

Two-stage Approach

Filtering (64 bit codes):
- Find all 64 bit codes with distance < 12
- Select 64 most important bits from 256 bit codes
- Apply Multi-Index Hashing:
  - Partition 64 bit codes into \(m=4\) subcodes
  - Within Hamming radius \(r=11\) at least one of the subcodes has distance \(d \leq \lfloor \frac{e}{m} \rfloor = 2\)
  - Searching subcode radii \(d=2\) much faster (ES inverted index)
Re-Ranking (256 bit codes):
- More accurate
- Hamming distance computation only on small subset

Indices

Documents in the retrieval index (e.g. images) are referenced to all \(d=2\) neighbors of their subcodes.

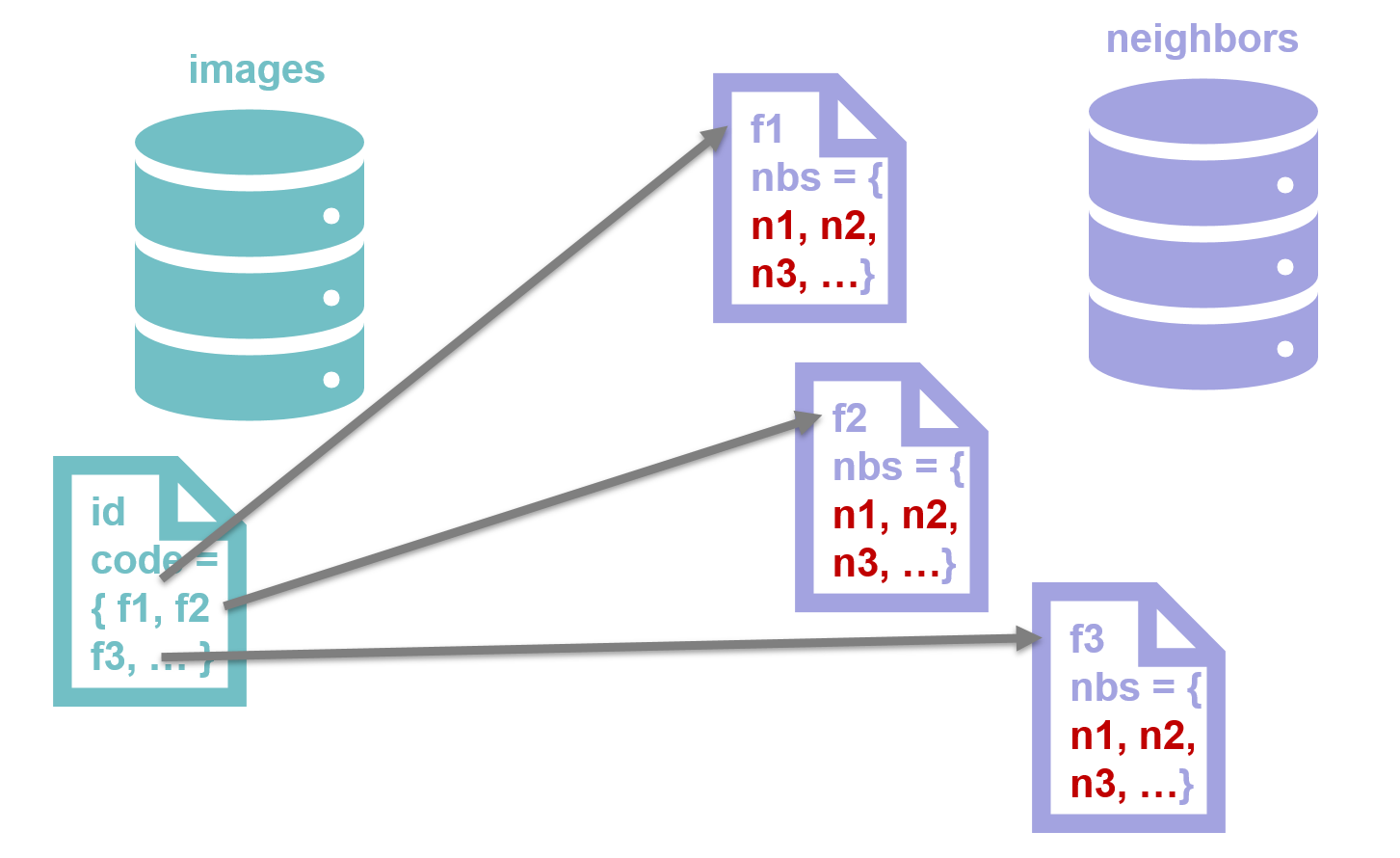
Queries

Painless Script for Hamming distance

Script for computing Hamming distance on 4 long int values:

# POST _scripts/hd64
{
  "script":
   {
     "lang": "painless",
     "source":
      64-Long.bitCount(params.subcodeˆdoc[params.field].value)
   }
}

Images Index

Short codes (f0... f3) are for filtering, long codes (r0... r3) for re-ranking.

# PUT /es-retrieval
# PUT /es-retrieval/default/_mapping

{
  "properties": {
    "image": {"type": "text"},
    "f0": {"type": "keyword"},
    "f1": {"type": "keyword"},
    "f2": {"type": "keyword"},
    "f3": {"type": "keyword"},
    "r0": {"type": "long"},
    "r1": {"type": "long"},
    "r2": {"type": "long"},
    "r3": {"type": "long"}
  }
}

Neighbors Index

Created once
Contains neighboring hashcodes for each subcode \(f_j\)
\(2^{16}\) documents (subcodes)

Example: all possible neighbors of \(01\) are \(01,10,00,11\), i.e. \(1,2,0,3\)

# POST/nbs-d2/_doc/<16 bit subcode>
{
  "nbs" : [ <d2 neighbors  of 16 bit  subcode> ]
}

Search Query

# GET /es-retrieval/_search
{ "query": { "function_score":  {"boost_mode": "sum", "score_mode": "sum", "functions":
  [ ..., { "script_score": {"script": {"id": "hd64",
    "params": {
    "field": "r_<i>",
    "subcode": <64 bit subcode for re-ranking>} } },
     "weight": 1}, ... ],

  "query": {"constant_score":{"boost": 0.,
    "filter":{"bool":{"minimum_should_match": 1,"should":      [..., {"terms":
        {"f_<j>":
          {"id": "<16 bit subcode for lookup>",
       "index": "nbs-d2",
           "path": "nbs"} } }, ... ]
} } } },} } }